大数法则和中心极限定理！

概要

如果想知道某个地区的平均收入是多少，应该怎么做？

如果遇到类似于上面的问题，应该如何科学的估计它，这就能够体现数学这门科学的强大了。

因为现实上想要调查所有样本往往都是困难的，所以对整体进行一个抽样调查，对于抽取的样本进行分析由此来对整体进行一个合理的估计。

假设抽取的样本为$$，满足独立同分布，则可以计算样本均值为$$。这边抽取多组样本就会存在多个样本均值$$，那么如果能够知道样本均值们是长什么样的话，就能够估计很多事情。

大数法则和中心极限定理的内容就是描述样本均值具有哪些数学性质。

大数法则 Law of Large Numbers

大数法则的描述

随着$$增加，样本均值逐渐接近总体的均值。

这里的接近一词，在数学上的含义就是收敛于此。

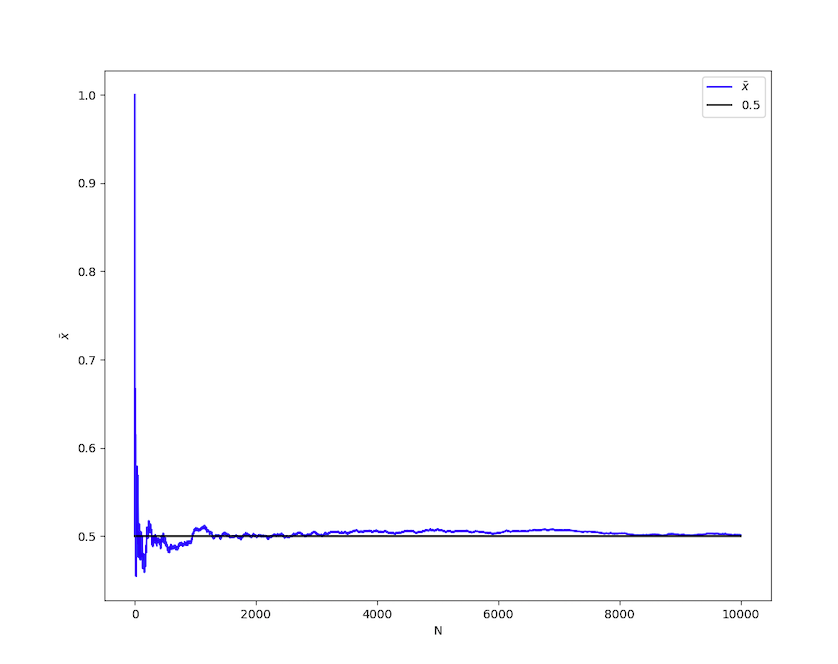
大数法则的模拟实验

这是一个抛硬币的模拟实验，总共抛10000次，并绘制样本均值$$。可以观察到最终样本均值逐渐趋向总体的均值0.5处收敛的样子。

大数弱法则数学证明的文章已经写好了，在大数弱法则证明。

数学证明已更新

大概思路是 Markov不等式 -> Chebyshev不等式 -> 大数法则的弱定律证明。
具体数学的证明将另外写一篇文章来说明。这篇文章主要以介绍大数定律的意义为主。

大数法则的意义

意义: 大数法则的意义在于，说明了一些随机事件的均值具有长期稳定的性质。

中心极限定律 Center Limit Theorem

中心极限定律的描述

随着$$增加，样本均值以总体均值为中心呈正态分布。

想知道样本均值们长什么样？因为知道长什么样了就能够了解它的数学性质。
而在数学上描述长什么样通常有三个问题，就是中心center、形状shape、分散spread。
而分布就能完美的回答上述问题。

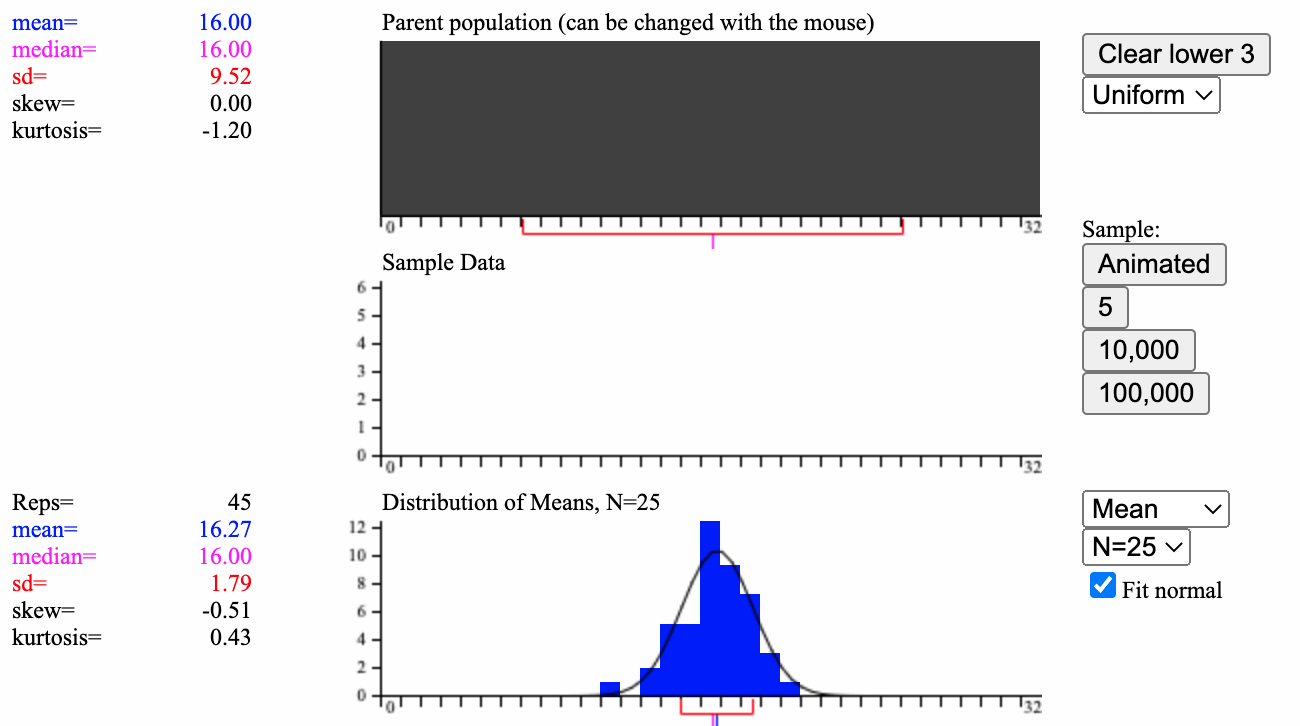
中心极限定律的模拟实验

这边推荐一个有趣的网站，可以进行中心极限定律的模拟实验。
模拟实验

本身提供一些正态分布、均一分布、偏正态分布，模拟抽样的过程并绘制样本均值的分布。也可以自己自定义原数据的分布情况。

这边可以观察到，当样本量增加时样本均值的分布是以总体均值为中心呈现正态分布的，这也印证了中心极限定理的内容。

数学证明待更新

关于中心极限定理中比较著名的证明二项分布的正态近似等将单独写一篇文章来整理。

中心极限定律的意义

意义: 中心极限定律的意义在于，只要样本量足够多就可以准确的预测总体的特征。

而当$$即可认为满足条件。夸张一点讲中心极限定理描述了万物皆可正态分布！

总结

大数法则主要描述了样本均值$$。
中心极限定理主要描述了样本均值$$周边以什么样子变化，也就是$$。